Risposte:

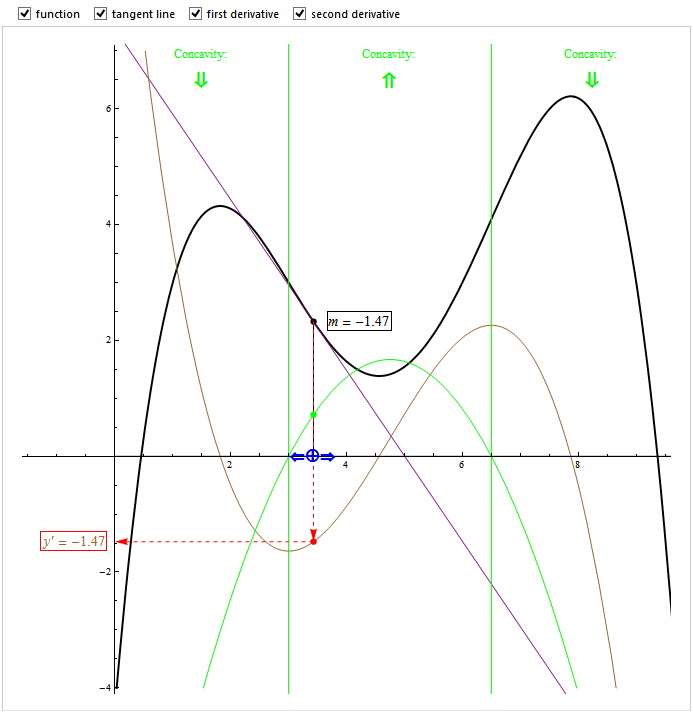
• quando la derivata prima è positiva la funzione è…
  crescente
  
• quando la funzione è decrescente la derivata prima è…
  negativa
  
• quando la derivata prima attraversa l’asse x la funzione ha…
  retta tangente orizzontale e un cambio di comportamento (da crescente a decrescente o viceversa). È quindi presente un massimo o un minimo relativo. Ma se la derivata prima non attraversa l’asse x ma solo lo “tocca” (essendo tangente all’asse x), allora la funzione ha un punto di flesso con tangente orizzontale.
  
• quando la funzione attraversa l’asse x la derivata prima è…
  qualsiasi.. e l’ordinata della derivata prima è semplicemente il coefficiente angolare della retta tangente alla funzione nel punto di attraversamento dell’asse x.
  
• quando la funzione ha un massimo (o un minimo) relativo la derivata prima…
  attraversa l’asse x (e il suo valore è 0, cioè )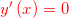  
  
• quando la derivata prima ha un massimo (o minimo) relativo la derivata seconda…
  attraversa l’asse x (e il suo valore è 0, cioè )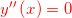
  
• quando la funzione ha la concavità rivolta verso l’alto (sorride) la derivata seconda è…
  positiva
  
• quando la funzione ha la concavità rivolta verso il basso (è triste) la derivata seconda è...
  negativa
  
• quando la derivata seconda è nulla la derivata prima… e la funzione…
  la retta tangente alla curva della derivata prima ha coefficiente angolare 0 e la funzione può avere un punto di flesso.
  Se la derivata seconda attraversa l’asse x allora la derivata prima ha un massimo o un minimo relativo e c’è in effetti un punto di flesso per la funzione.
  Ma se la derivata seconda è solamente tangente all’asse x (e la tocca senza attraversarla) allora le cose sono più complicate e bisogna analizzare le derivate successive…
  
• quando la derivata seconda è positiva (negativa) la derivata prima… e la funzione…
  la derivata prima è crescente (decrescente) e la funzione ha la concavità diretta verso l’alto (verso il basso)

[torna alla dimostrazione Visualizzazione della derivata prima e seconda di una funzione]